Bracket-matching application

Now let's look at an example of how we can use our stack implementation.

• We are going to write a little function that will verify whether a statement containing brackets--(, [, or {--is balanced, that is, whether the number of closing brackets matches the number of opening brackets.

It will also ensure that one pair of brackets really is contained in another:

def check_brackets(statement):
    stack = Stack()
    for ch in statement:
        if ch in ('{', '[', '('):
            stack.push(ch)
        if ch in ('}', ']', ')'):
            last = stack.pop()
        if last is '{' and ch is '}':
            continue
        elif last is '[' and ch is ']':
            continue
        elif last is '(' and ch is ')':
            continue
        else:
            return False
if stack.size > 0:
    return False
else:
    return True
    

Our function parses each character in the statement passed to it. If it gets an open bracket, it pushes it onto the stack. If it gets a closing bracket, it pops the top element off the stack and compares the two brackets to make sure their types match: ( should match ), [ should match ], and { should match }. If they don't, we return False, otherwise we continue parsing.

Once we have got to the end of the statement, we need to do one last check. If the stack is empty, then we are fine and we can return True. But if the stack is not empty, then we have some opening bracket which does not have a matching closing bracket and we shall return False. We can test the bracket-matcher with the following little code:

s1 = (
    "{(foo), (bar) } [hello] (((this) is) a) test",
    "{(foo), (bar) } [hello] (((this) is) atest",
    "{(foo), (bar) } [hello] (((this) is) a) test))"
)
for s in s1:
    m = check_brackets(s)
    print("{}: {}".format(s, m));
    

Only the first of the three statements should match. And when we run the code, we get the following output:

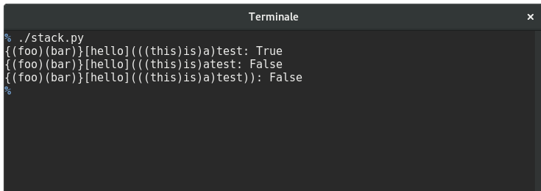
True, False, False. The code works. In summary, the push and pop operations of the stack data structure attract a O(1). The stack data structure is simply enough but is used to implement a whole range of functionality in the real world. The back and forward buttons on the browser are made possible by stacks. To be able to have undo and redo functionality in word processors, stacks are also used.